W5500 TCP Function
By setting some register and memory operation, W5500 provides internet connectivity. This chapter describes how it can be operated.
Initialization
You must check PHY LINK (0 bit of PHYCFGR) before attempting to make a network connection using sockets.
Basic Setting
For the W5500 operation, select and utilize appropriate registers shown below.
- Mode Register (MR)
- Interrupt Mask Register (IMR)
- Retry Time-value Register (RTR)
- Retry Count Register (RCR)
For more information of above registers, refer to the “Register Descriptions.”
Setting network information
Basic network information setting for communication: It must be set the basic network information.
- SHAR(Source Hardware Address Register)
- It is prescribed that the source hardware addresses, which is set by SHAR, use unique hardware addresses (Ethernet MAC address) in the Ethernet MAC layer. The IEEE manages the MAC address allocation. The manufacturer which produces the network device allocates the MAC address to product.
- Details on MAC address allocation refer to the website as below.
- 🌎http://www.ieee.org/
- 🌎http://standards.ieee.org/regauth/oui/index.shtml
- GAR(Gateway Address Register)
- SUBR(Subnet Mask Register)
- SIPR(Source IP Address Register)
Set socket memory information
This stage sets the socket tx/rx memory information. The base address and mask address of each socket are fixed and saved in this stage.
In case of, assign 2KB rx, tx memroy per SOCKET
In case of, assign 2KB rx, tx memory per SOCKET
{
Sn_RXMEM_SIZE(ch) = (uint8 *) 2; // Assign 2K rx memory per SOCKET
Sn_TXMEM_SIZE(ch) = (uint8 *) 2; // Assign 2K rx memory per SOCKET
/* Same method, set gS1_TX_BASE, gS1_TX_MASK, gS2_TX_BASE, gS2_TX_MASK,
gS3_TX_BASE, gS3_TX_MASK, gS4_TX_BASE, gS4_TX_MASK, gS5_TX_BASE, gS5_TX_MASK,
gS6_TX_BASE, gS6_tx_MASK, gS7_TX_BASE, gS7_TX_MASK */
}
Data Communications
After the initialization process, W5500 can transmit and receive the data with others by ‘open’ the SOCKET of TCP, UDP, IPRAW, and MACRAW mode. The W5500 supports the independently and simultaneously usable 8 SOCKETS. In this section, the communication method for each mode will be introduced.
TCP
The TCP is a connection-oriented protocol. The TCP make the connection SOCKET by using its own IP address, port number and destination IP address, port number. Then transmits and receives the data by using this SOCKET. Methods of making the connection to SOCKET are “TCP SERVER” and “TCP CLIENT”. It is divided by transmitting the connect-request (SYN packet). The “TCP SERVER” listens to the connect-request from the “TCP CLIENT”, and makes connection SOCKET by accepting the transmitted connect-request (Passive-open). The “TCP CLIENT” transmits the connect-request first to “TCP SERVER” to make the connection (Active-open).
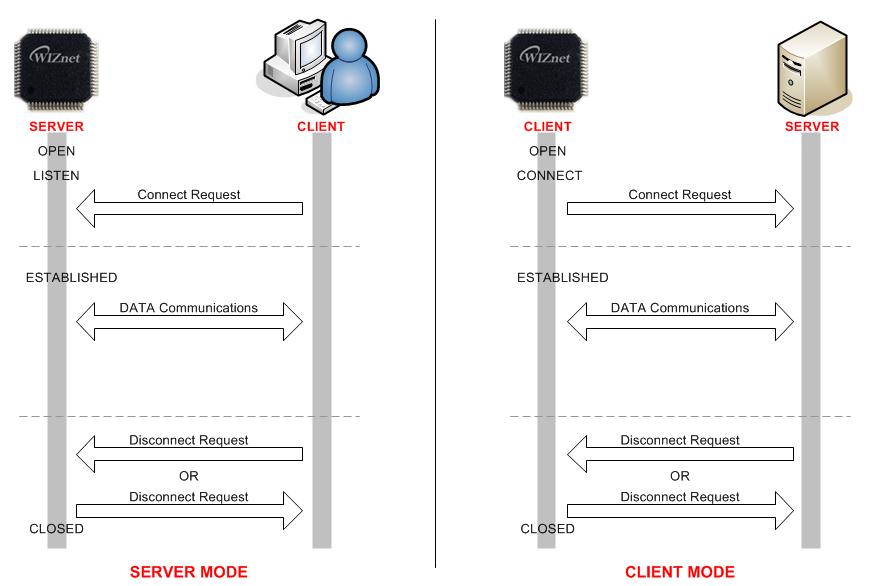
TCP SERVER
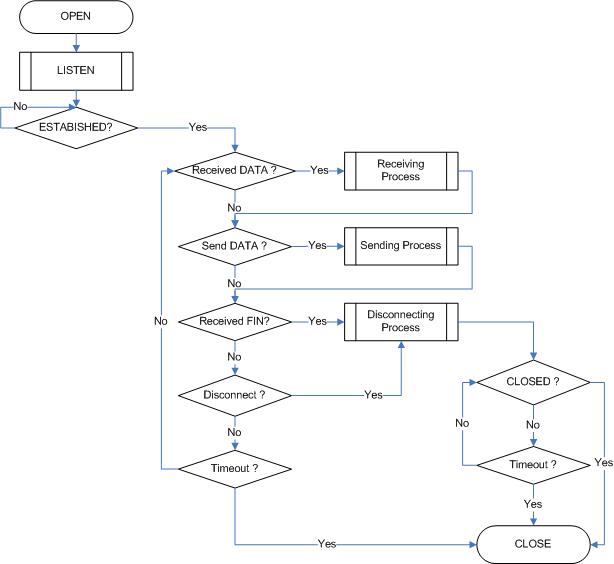
SOCKET Initialization
SOCKET initialization is required for TCP data communication. The initialization is opening the SOCKET. The SOCKET opening process selects one SOCKET from 8 SOCKETS of the W5500, and sets the protocol mode (Sn_MR) and Sn_PORT0 which is source port number (Listen port number in “TCP SERVER”) in the selected SOCKET, and then executes OPEN command. After the OPEN command, if the status of Sn_SR is changed to SOCK_INIT, the SOCKET initialization process is completed. The SOCKET initialization process is identically applied in “TCP SERVER” and “TCP CLIENT.”The Initialization process of Socket n in TCP mode is shown below.
{
START:
Sn_MR = 0x01; // sets TCP mode
Sn_PORT0 = source_port; // sets source port number
Sn_CR = OPEN; // sets OPEN command
/* wait until Sn_SR is changed to SOCK_INIT */
if (Sn_SR != SOCK_INIT) Sn_CR = CLOSE; goto START;
}
After W5500 accepts the command, the Sn_CR register is automatically cleared to 0x00. Even though Sn_CR is cleared to 0x00, the command is still being processed. To check whether the command is completed or not, please check the Sn_IR or Sn_SR.
LISTEN
Run as “TCP SERVER” by LISTEN command.
{
/* listen SOCKET */
Sn_CR = LISTEN;
/* wait until Sn_SR is changed to SOCK_LISTEN */
if (Sn_SR != SOCK_LISTEN) Sn_CR = CLOSE; goto START;
}
ESTABLISHMENT
When the status of Sn_SR is SOCK_LISTEN, if it receives a SYN packet, the status of Sn_SR is changed to SOCK_SYNRECV and transmits the SYN/ACK packet. After that, the Socket n makes a connection. After it makes the connection of Socket n , it enables the data communication. There are two methods to confirm the connection of Socket n .
First method :
{
if (Sn_IR(CON) == ‘1’)
/* When an interrupt occurs and the mask bit of Sn_IMR is ‘1’, the interrupt bit of Sn_IR
becomes ‘1’ */
Sn_IR(CON) = ‘1’;
/*In order to clear the Sn_IR bit, the host should write the bit as ‘1’. When all the bits of
Sn_IR is cleared (‘0’), IR(n) is automatically cleared.*/
goto ESTABLISHED stage;
/* In this case, if the interrupt of Socket n is activated, interrupt occurs. Refer to IR, IMR
Sn_IMR and Sn_IR. */
}
Second method :
{
if (Sn_SR == SOCK_ESTABLISHED) goto ESTABLISHED stage;
}
ESTABLISHMENT : Check received data
Confirm the reception of the TCP data.
First method :
{
if (Sn_IR(RECV) == ‘1’) Sn_IR(RECV) = ‘1’; goto Receiving Process stage;
/* In this case, if the interrupt of Socket n is activated, interrupt occurs. Refer to IR, IMR
Sn_IMR and Sn_IR. */
}
Second Method :
{
if (Sn_RX_RSR0 != 0x0000) goto Receiving Process stage;
}
The First method: set the Sn_IR(RECV) to ‘1’ whenever you receive a DATA packet. If the host receives the next DATA packet without setting the Sn_IR(RECV) as ‘1’ in the prior DATA packet, it cannot recognize the Sn_IR(RECV) of the next DATA packet. This is due to the prior Sn_IR(RECV) and next Sn_IR(RECV) being overlapped. So this method is not recommended if the host cannot perfectly process the DATA packets of each Sn_IR(RECV).
ESTABLISHMENT : Receiving process
In this process, it processes the TCP data which was received in the Internal RX memory. At the TCP mode, the W5500 cannot receive the data if the size of received data is larger than the RX memory free size of Socket n . If the prior stated condition is happened, the W5500 holds on to the connection (pauses), and waits until the RX memory’s free size is larger than the size of the received data.
{
/* first, get the received size */
len = Sn_RX_RSR; // len is received size
/* select RX memory, refer to Datasheet 14 page */
cntl_byte = Socket_n_RX_Buffer
/* Get offset address */
src_ptr = Sn_RX_RD;
/* set memory copy len bytes of source_ptr to destination_address */
for (i=0; i<len; i++)
{
*(dst_ptr+i) = W5500_READ(addr, cntl_byte, src_ptr+i);
}
/* increase Sn_RX_RD as length of len */
Sn_RX_RD += len;
/* set RECV command */
Sn_CR = RECV;
}
ESTABLISHMENT: Check send data / Send process
The size of the transmit data cannot be larger than assigned internal TX
memory of Socket n. If the size of transmit data is larger than
configured MSS, it is divided by size of MSS and transmits. To transmit
the next data, user must check the completion of prior SEND command. An
error may occur if the SEND command executes before completion of prior
SEND command. The larger the data size, the more time to complete the
SEND command. So the user should properly divide the data to transmit.
To check the completion of the SEND command, it should be check that the
send data length is equal with the actual sent data length. The actual
sent data length is calculated by the difference of the Sn_TX_RD
before and after performing the SEND command. If the actual sent data is
less than the send data length, the SEND command is retried for sending
the left data. The send process is therefore completed the SENDwhen the
sum of the actual sent data is equal the send data length. A simple
example of the send process is as below
Ex) Send Data Length Size= 10,
- Execute SEND Command with send data length
- Calculate the actual sent data length
- If the actual sent data length is 7 (= Sn_TX_RD_after_SEND-Sn_TX_RD_befor_SEND),
- the left Data length= 3
- Retry SEND Command until the sum of the actual sent data length is
same the send data length.
Note: Don’t copy data until the sum of the actual sent data length is the send data length.
{
/* first, get the free TX memory size */
FREESIZE:
freesize = Sn_TX_FSR;
if (freesize<len) goto FREESIZE; // len is send size
/* select TX memory, refer to Datasheet 14 page */
cntl_byte = Socket_n_TX_Buffer
/* Get offset address */
dst_ptr = Sn_TX_RD;
/* set memory copy len bytes of source_ptr to destination_address */
for (i=0; i<len; i++)
{
W5500_WRITE(addr, cntl_byte, dst_ptr+i);
}
/* increase Sn_TX_WR as length of len */
Sn_TX_WR += send_size;
/* set SEND command */
Sn_CR = SEND;
/* return real packet size */
return len;
}
ESTABLISHMENT : Check disconnect-request(FIN packet)
Check if the Disconnect-request(FIN packet) has been received. User can confirm the reception of FIN packet as below.
First method :
{
if (Sn_IR(DISCON) == ‘1’) Sn_IR(DISCON)=‘1’; goto CLOSED stage;
/* In this case, if the interrupt of Socket n is activated, interrupt occurs. Refer to IR, IMR
Sn_IMR and Sn_IR. */
}
Second method :
{
if (Sn_SR == SOCK_CLOSE_WAIT) goto CLOSED stage;
}
ESTABLISHMENT : Check disconnect / disconnecting process
When the user does not need data communication with others, or receives a FIN packet, disconnect the connection SOCKET.
{
/* set DISCON command */
Sn_CR = DISCON;
}
ESTABLISHMENT : Check closed
Confirm that the Socket n is disconnected or closed by DISCON or close command.
First method :
{
if (Sn_IR(DISCON) == ‘1’) goto CLOSED stage;
/* In this case, if the interrupt of Socket n is activated, interrupt occurs. Refer to IR, IMR
Sn_IMR and Sn_IR. */
}
Second method :
{
if (Sn_SR == SOCK_CLOSED) goto CLOSED stage;
}
ESTABLISHMENT: Timeout
The timeout can occur by Connect-request(SYN packet) or its response(SYN/ACK packet), the DATA packet or its response(DATA/ACK packet), the Disconnect request FIN packet) or its response(FIN/ACK packet) and transmission all TCP packet. If it cannot transmit the above packets within ‘timeout’ which is configured at RTR and RCR, the TCP final timeout(TCPTO) occurs and the state of Sn_SR is set to SOCK_CLOSED. Confirming method of the TCPTO is as below:
First method :
{
if (Sn_IR(TIMEOUT bit) == ‘1’) Sn_IR(TIMEOUT)=‘1’; goto CLOSED stage;
/* In this case, if the interrupt of Socket n is activated, interrupt occurs. Refer to IR, IMR
Sn_IMR and Sn_IR. */
}
Second method :
{
if (Sn_SR == SOCK_CLOSED) goto CLOSED stage;
}
SOCKET Close
It can be used to close the Socket n , which disconnected by disconnect-process, or closed by TCPTO or closed by host’s need without disconnect-process.
{
/* clear the remained interrupts of Socket n */
Sn_IR = 0xFF;
IR(n) = ‘1’;
/* set CLOSE command */
Sn_CR = CLOSE;
}
TCP CLIENT
It is same as TCP server except ‘CONNECT’ state. User can refer to the above "TCP SERVER” section.
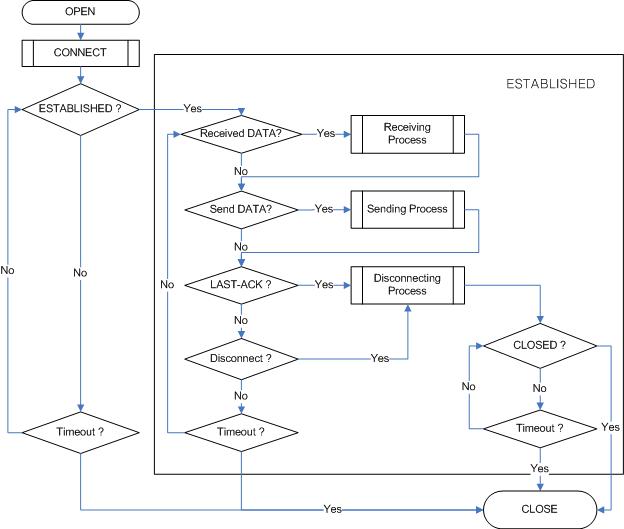
CONNECT
Transmit the connect-request (SYN packet) to “TCP SERVER”. It may occurs the timeout such as ARPTO, TCPTO when make the “connection SOCKET” with “TCP SERVER”
{
Sn_DIPR0 = server_ip; /* set TCP SERVER IP address*/
Sn_DPORT0 = server_port; /* set TCP SERVER listen port number*/
Sn_CR = CONNECT; /* set CONNECT command */
}